Switched capacitor filter (SCF) or analog Sampled data or commutating filter 

 Switched capacitor Filters (SCFs) are active IC filters made of op amps, capacitors, and transistor switches. Also known as analog sampled data Filters or commutating filters, these devices are usually implemented with MOS or CMOS circuits. They can be designed to operate as high-pass, low-pass, bandpass, or bandstop filters. The primary advantage of SCFs is that they provide a way to make tuned or selective circuits in an IC without the use of discrete inductors, capacitors, or resistors. 
Switched capacitor filters are made of op amps, MOSFET switches, and capacitors. All components are fully integrated on a single chip, making external discrete components unnecessary. The secret to the SCF is that all resistors are replaced by capacitors that are switched by MOSFET switches. Resistors are more dificult to make in IC form and take up far more space on the chip than transistors and capacitors. With switched capacitors, it is possible to make complex active i lters on a single chip. Other advantages are selectibility of filter type, full adjustability of the cutoff or center frequency, and full adjustability of bandwidth. One filter circuit can be used for many different applications and can be set to a wide range of frequencies and bandwidths. 
  
Switched Integrators. The basic building block of SCFs is the classic op amp integrator, as shown in Fig. 1-01(a). The input is applied through a resistor, and the feedback is provided by a capacitor. With this arrangement, the output is a function of the integral of the input: 
With ac signals, the circuit essentially functions as a low-pass filter with a gain of 1/RC. 

Figure 1-01 IC integrators. (a) Conventional integrator. (b) Switched capacitor integrator 
To work over a wide range of frequencies, the integrator RC values must be changed. Making low and high resistor and capacitor values in IC form is dificult. However, this problem can be solved by replacing the input resistor with a switched capacitor, as shown in Fig. 1-01(b). The MOSFET switches are driven by a clock generator whose frequency is typically 50 to 100 times the maximum frequency of the ac signal to be i ltered. The resistance of a MOSFET switch when on is usually less than 1000 V. When the switch is off, its resistance is many megohms. 

     The clock puts out two phases, designated ϕ1 and ϕ2 , that drive the MOSFET switches. When S1 is on, S2 is off and vice versa. The switches are of the break- beforemake type, which means that one switch opens before the other is closed. When S1 is closed, the charge on the capacitor follows the input signal. Since the clock period and time duration that the switch is on are very short compared to the input signal variation, a brief “sample” of the input voltage remains stored on C1 and S1 turns off. 

       Now S2 turns on. The charge on capacitor C1 is applied to the summing junction of the op amp. It discharges, causing a current to Flow in the feedback capacitor C2 . The resulting output voltage is proportional to the integral of the input. But this time, the gain of the integrator is  

 where 𝒇 is the clock frequency. Capacitor C1 , which is switched at a clock frequency of 𝒇 with period T, is equivalent to a resistor value of R 5 T/C1 . 
   The beauty of this arrangement is that it is not necessary to make resistors on the IC chip. Instead, capacitors and MOSFET switches, which are smaller than resistors, are used. Further, since the gain is a function of the ratio of C1 to C2 , the exact capacitor values are less important than their ratio. It is much easier to control the ratio of matched pairs of capacitors than it is to make precise values of capacitance. 
    By combining several such switching integrators, it is possible to create low-pass, high-pass, bandpass, and band-reject Filters of the Butterworth, Chebyshev, elliptical, and Bessel type with almost any desired selectivity. The center frequency or cutoff frequency of the Filter is set by the value of the clock frequency. This means that the filter can be tuned on the l y by varying the clock frequency 
      A unique but sometimes undesirable characteristic of an SCF is that the output signal is really a stepped approximation of the input signal. Because of the switching action of the MOSFETs and the charging and discharging of the capacitors, the signal takes on a stepped digital form. The higher the clock frequency compared to the frequency of the input signal, the smaller this effect. The signal can be smoothed back into its original state by passing it through a simple RC low-pass i lter whose cutoff frequency is set to just above the maximum signal frequency. 
     Various SCFs are available in IC form, both dedicated single-purpose or universal versions. Some models can be coni gured as Butterworth, Bessel, Eliptical, or other formats with as many as eight poles. They can be used for  filtering signals up to about 100  kHz. Manufacturers include Linear Technology, Maxim Integrated Products, and Texas Instruments. One of the most popular is the MF10 made by Texas Instruments. It is a universal SCF that can be set for low-pass, high-pass, bandpass, or band-reject operation. It can be used for center or cutoff frequencies up to about 20 kHz. The clock frequency is about 50 to 100 times the operating frequency. 
    Commutating Filters. An interesting variation of a switched capacitor filter is the commutating filter shown in Fig. 1-02. It is made of discrete resistors and capacitors with MOSFET switches driven by a counter and decoder. The circuit appears to be a low-pass RC filter, but the switching action makes the circuit function as a bandpass filter. The operating frequency fout is related to the clock frequency fc and the number N of switches and capacitors used.  
Figure 1-02 A commutating SCF. 



 The bandwidth of the circuit is related to the RC values and number of capacitors and switches used as follows: 
 
For the filter in Fig. 1-02, the bandwidth is BW = 1/(8πRC). 
Very high Q and narrow bandwidth can be obtained, and varying the resistor value makes the bandwidth adjustable 
    The operating waveforms in Fig. 1-02 show that each capacitor is switched on and off sequentially so that only one capacitor is connected to the circuit at a time. A sample of the input voltage is stored as a charge on each capacitor as it is connected to the input. The capacitor voltage is the average of the voltage variation during the time the switch connects the capacitor to the circuit. 
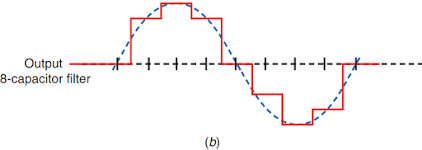
          Fig. 1-03(a) shows typical input and output waveforms, assuming a sine wave input. The output is a stepped approximation of the input because of the sampling action of the switched capacitors. The steps are large, but their size can be reduced by simply using a greater number of switches and capacitors. Increasing the number of capacitors from four to eight, as in Fig. 1-03(b), makes the steps smaller, and thus the output more closely approximates the input. The steps can be eliminated or greatly minimized by passing the output through a simple RC low-pass filter whose cutoff is set to the center frequency value or slightly higher 
          One characteristic of the commutating filter is that it is sensitive to the harmonics of the center frequency for which it is designed. Signals whose frequency is some integer multiple of the center frequency of the filter are also passed by the filter, although 

Figure 1-03 Input and output for commutating filter. (a) Four-capacitor filter. (b) Eight-capacitor filter. 

Figure 1-04 Comb filter response of a commutating filter. 
at a somewhat lower amplitude. The response of the filter, called a comb response, is shown in Fig. 1-04. If such performance is undesirable, the higher frequencies can be eliminated with a conventional RC or LC low-pass filter connected to the output.